how-toteach-long-division So, your child has mastered their times tables and now they’re moving onto long division. Long division may seem easy, but in fact, it can be quite difficult to teach and to understand. Let’s break down how to understand long division.

The Steps of Long Division

Divide
Multiply
Subtract
Drop down

Before We Begin

Before we can teach long division we must understand the terms associated with it. The number being divided is called the dividend, the number that is dividing is called the divisor, and lastly the number that is the answer of the division problem is called the quotient. Bonus: if the divisor does not divide evenly into the dividend there will be a remainder left over.

For example

3234 ÷ 6 = 539

3234 is being divided by 6, which is the same as saying 6 is dividing 3234. The answer to this division problem is 539 or 539 is the quotient of 3234 divided by 6.

But if we had 3237 ÷ 6 our answer would be 539 with a remainder of 3, 3237÷6=539 R3

STEP 1: DIVIDE

Okay, let’s go back to 3234÷6. In long division format it will look like

3234 divided by 6

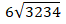
Make sure you do not say “six divided by three thousand two hundred thirty-four” which would look like

6 divided by 3234

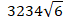
First, take a look at the left-most digit of the dividend.

Try to divide 3 by 6

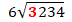
Ask your child “can 6 go into 3?” No, it is too small. Now you need to combine the next place value, the 2 (hundred), to the 3 (thousand) place value (3200).

Divide 32 by 6

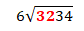
Can 6 go into 32? Yes, it can. Here is the first tripping point for a lot of students. 32 is not a multiple of 6 but it can be divided by 6 with something left over. When you are going over this with your child and they say that 32 cannot be divided by 6 they are not wrong.

You can ask your child “how many groups of 6 can you make from 32?” They can draw 32 circles and group them into groups of 6, after making 5 groups they will see that there is only 2 circles left over and they can only make 5 groups of 6 out of 32. However, as they get more practice with long division they need to be able to imagine the groups in their head and conclude that they can make 5 groups of 6 without having to draw out circles.

Alternatively, you can ask them “what is a multiple of 6 that is closest to 32?” They will answer 30. Great! Now ask, “what is 30 divided by 6?” They will answer 5.

STEP 2: MULTIPLY

Your child now knows that 6 can go into 32 at most 5 times. What next? Multiply. 5x6 =30. The 5 goes on top of the answer bar as the first number of our answer. The 30 goes underneath the dividend to prepare for Step 3.

Multiply 5 by 6

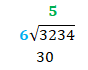
STEP 3: SUBTRACT

Next we subtract 32-30=2. In the long division this looks like

Subtract 32-30=2

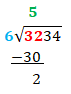
STEP 4: BRING DOWN

We have to do something with this 2 left over now. 6 cannot go into 2, as your child will gladly confirm. Now we Bring Down the next digit of the dividend and our new dividend is 23

Bring down the 3 to make 23

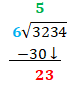
REPEAT

Start back at STEP 1. Can 6 go into 23? Yes 3 times. STEP 2, what is 3 x 6? 18. STEP 3, What is 23-18? 5. STEP 4 bring down the 4.

Start back at Step 1 and Repeat

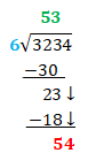
NOW YOU TRY

Can 6 go into 54? How many times? Where does the 9 go? What’s next? Subtract 54-54=0. Is there anything left to bring down?

Now you try

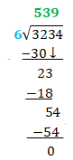
Well then, it looks like we are all done and you know how to explain long division! Even though for some students it is difficult and hard to understand, with this method your child will be doing long division in no time. Here are some helpful long division sheets to practice at home.